Tìm cực trị của hàm số là một trong những dạng toán rất thường gặp. Vậy có bao nhiêu dạng bài toán cực trị và làm thế nào để giải được các bài toán đó? Theo dõi bài viết dưới đây để trang bị thêm cho mình những kiến thức hữu ích.
Dạng 1: Bài toán tìm cực trị của hàm số
Với dạng bài toán tìm cực trị của hàm số f(x)các bạn có thể giải theo 2 phương pháp sau:
Phương pháp 1:
- Tìm đạo hàm f'(x)
- Xác định các điểm xa (a=1;2;3...)tại đó đạo hàm bằng ) hoặc hàm số liên tục không có đạo hàm
- Xét dấu f'(x). Nếu f'(x) đổi dấu khi x qua xathì hàm số đạt cực trị tại điểm đó
Phương pháp 2:
- Tìm đạo hàm f'(x)
- Tìm nghiệm xa (a=1;2;3...) của phương trình f'(x)= 0
- Xét các tình huống
- Nếu f''(x)< 0 thì hàm số đạt cực đại tại điểm xa
- Nếu f''(x)> 0 thì hàm số đạt cực tiểu tại điểm xa
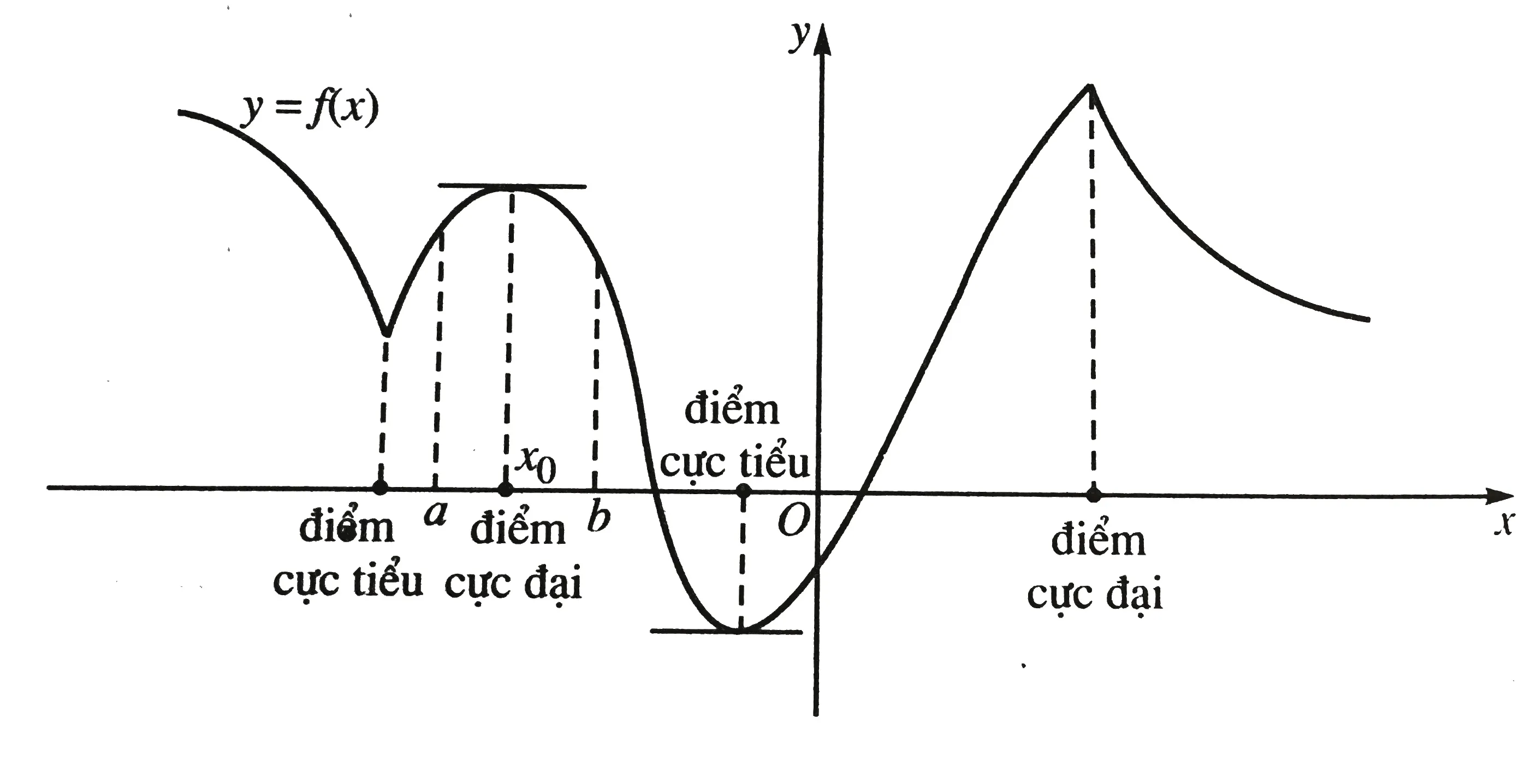
Ảnh 1: Ảnh minh họa
Ví dụ minh họa

Dạng 2: Phương trình đường thẳng đi qua 2 điểm cực đại và cực tiểu
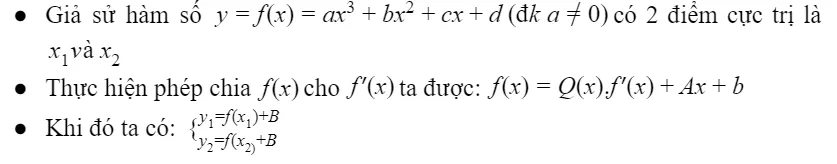
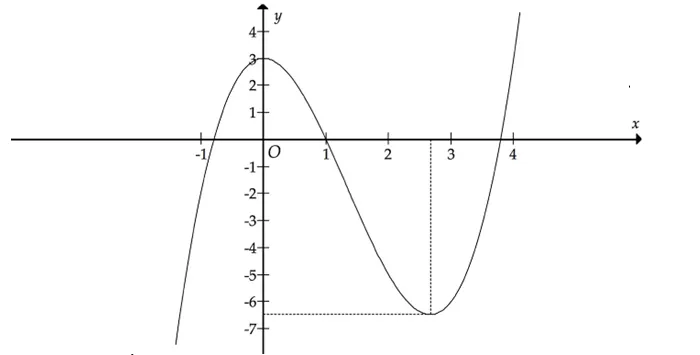
Ảnh 2: Ảnh minh họa cực trị của hàm số
Ví dụ minh họa


Dạng 3: Bài toán tìm cực trị hàm số bậc 3
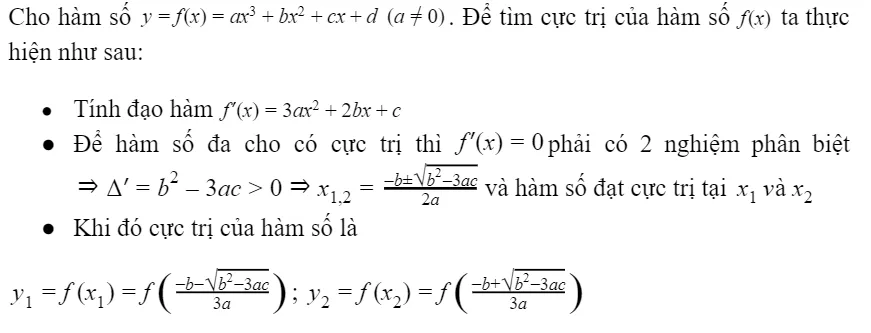


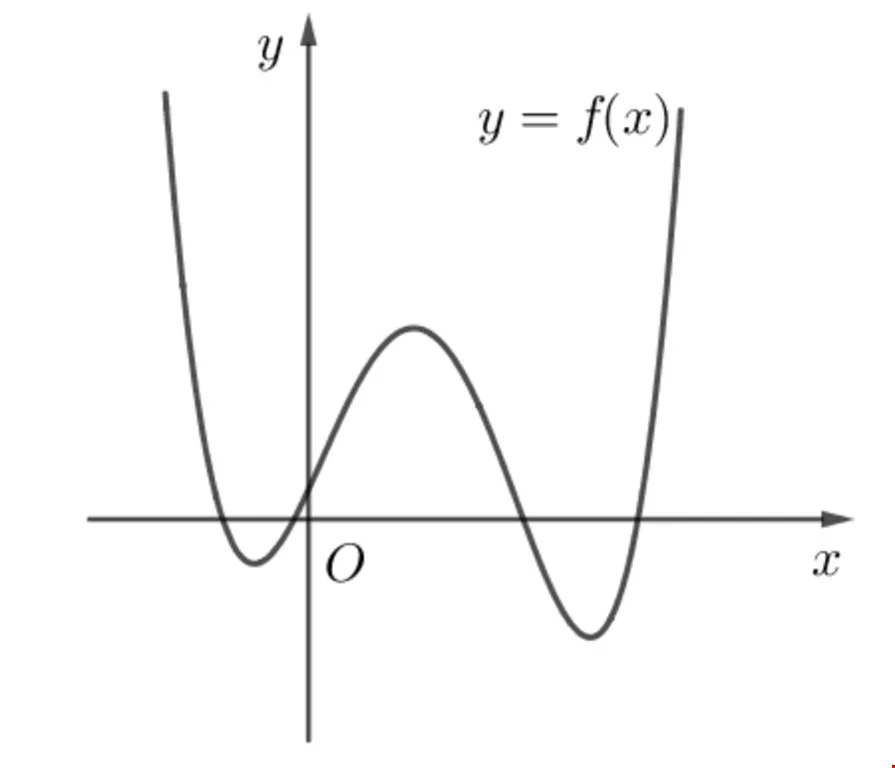
Ảnh 3: Ảnh minh họa cực trị của hàm số
Dạng 4: Bài toán tìm cực trị hàm trùng phương

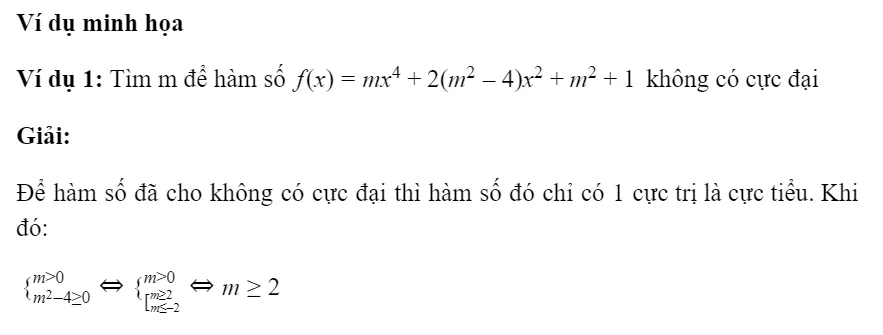
Trên đây là các dạng bài toán cực trị cũng như chi tiết cách giải của từng dạng. Hy vọng qua những kiến thức đã chia sẻ có thể giúp bạn hiểu hơn về phần kiến thức này và áp dụng một cách hiệu quả.
Nguồn ảnh: Internet
Cách lập bảng biến thiên hàm số: Khảo sát và vẽ đồ thị hàm số và vẽ bảng biến thiên là một dạng bài tập đơn giản và cơ bản nhất trong chương trình trung học phổ thông.
Kiến thức quan trọng về khảo sát sự biến thiên và vẽ đồ thị hàm số : Khảo sát và vẽ đồ thị hàm số là câu hỏi quen thuộc nằm trong các đề thi tốt nghiệp môn Toán từ xưa đến nay. Bài viết sau đây giúp các bạn học sinh nắm rõ hơn kiến thức về khảo sát hàm số.



