Hệ thức lượng trong tam giác vuông được coi là nền tảng vô cùng quan trọng cho việc học sau này. Vì vậy, các bạn cần phải nắm chắc những kiến thức cơ bản về nó. Bài viết này sẽ giúp các bạn củng cố lại những kiến thức về hệ thức lượng trong tam giác vuông.
Hệ thức lượng trong tam giác vuông
Đầu tiên chúng ta sẽ ôn lại những hệ thức lượng trong tam giác vuông:

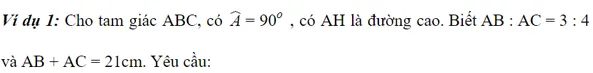
- Tính các cạnh của tam giác ABC.
- Tính độ dài các đoạn AH, BH và CH.
Bài giải:
- Theo giả thiết của đề bài ta có: AB : AC = 3 : 4 và AB + AC = 21cm,
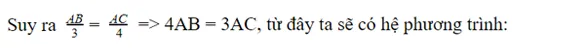
4AB = 3AC
AB + AC = 21
Suy ra AB = 9cm và AC = 12cm.
Vì tam giác ABC vuông tại A, Áp dụng định lý Pitago ta được:

Ví dụ 2: Cho tam giác cân ABC, có đáy BC = 4a, cạnh bên AB = AC =b (b>a). Yêu cầu:


Tỉ số lượng giác trong tam giác vuông
Ảnh minh họa (Nguồn: CIE Team)

Các tỉ số lượng trong tam giác vuông được định nghĩa như sau:
Nếu hai góc phụ bằng nhau thì sin góc này bằng cos góc kia, tang góc này bằng với cotan góc kia, được kí hiệu như sau:
- sinA = sinB
- cosA = sinB
- tanA = cotB
- cotgA = tanB
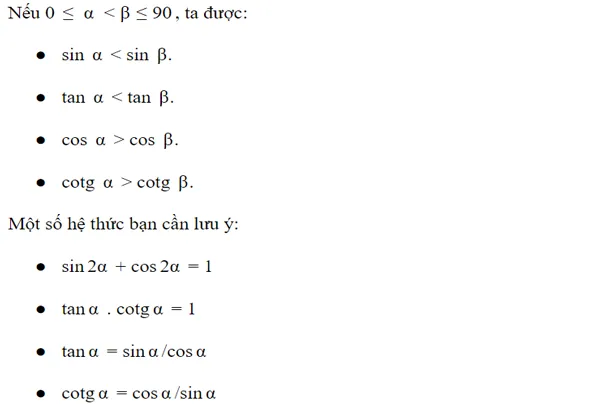
Một số bài toán mẫu về hệ thức lượng trong tam giác.
Bài 1: Cho tam giác nhọn ABC có AH và BK là 2 đường cao cắt nhau tại điểm E. Biết EH : EA = 1 : 2. Yêu cầu chứng minh tanB.tanC = 3.
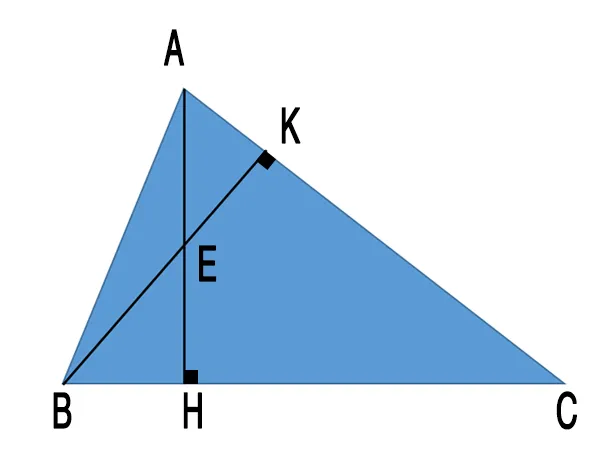
Ảnh bài 1 (Nguồn: CIE Team)


- Tính độ dài cạnh BC.
- Tính diện tích tam giác ABC.
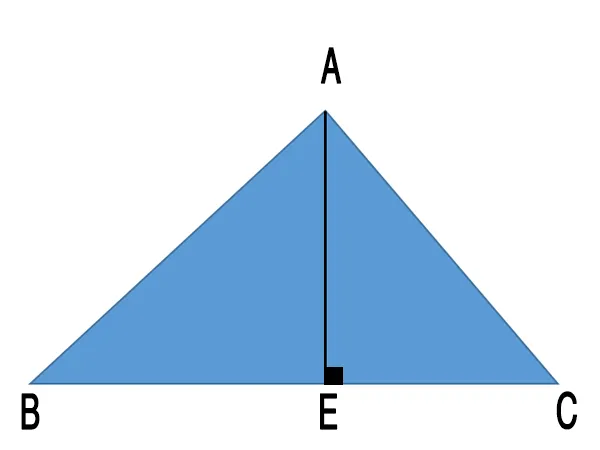
Ảnh bài 2 (Nguồn: CIE Team)
Bài giải:
- Vẽ đường cao AE.
Áp dụng định lý Pitago vào tam giác vuông AEC ta được:
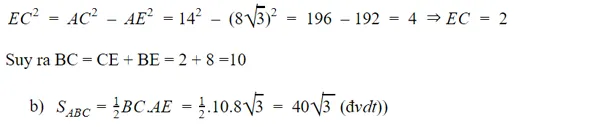
Bên trên là chia sẻ về những lý thuyết và các hệ thức trong tam giác. Hy vọng bài viết này sẽ giúp ích cho các bạn trong quá trình học tập.


