Tích phân suy rộng là một trong những phần kiến thức rất quan trọng của toán cao cấp. Bài viết dưới đây sẽ giúp các bạn tìm hiểu về hơn về phần kiến thức này.
Các loại tích phân suy rộng
Hiểu theo nghĩa thông thường tích phân suy rộng là giới hạn của tích phân xác định khi cho cận tích phân dần tới vô cùng. Tích phân suy rộng bao gồm 2 loại là tích phân suy rộng với cận vô hạn (tích phân suy rộng loại 1) và Tích phân suy rộng của hàm số không bị chặn (tích phân suy rộng loại 2)
Một số tính chất của tích phân suy rộng

Ảnh 1: Tính chất của tích phân suy rộng
Tích phân suy rộng loại 1
Giả sử f(x)là hàm số xác định trên khoảng a,+và khả tích trên mọi đoạn hữu hạn a,A, aA<+khi đó ta có định nghĩa:

Ảnh 2: Định nghĩa tích phân suy rộng loại 1
Để hiểu hơn về định nghĩa tích phân suy rộng loại 1 các bạn có thể tham khảo một số ví dụ sau:

Ảnh 3: Ví dụ minh họa tích phân suy rộng loại 1
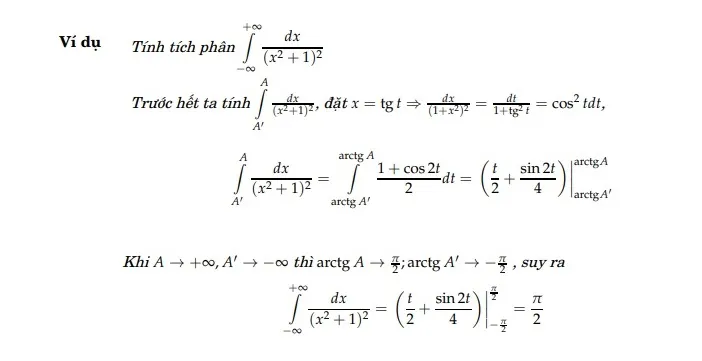
Ảnh 4: Ví dụ minh họa tích phân suy rộng loại 1
Tích phân suy rộng loại 2
Cho hàm sốf(x)là hàm số xác định trên khoảng [a.b)và khả tích trên [a,t] với mọi a<t<b, khi đó ta có định nghĩa:

Ảnh 5: Định nghĩa tích phân suy rộng loại 2
Để hiểu hơn về định nghĩa tích phân suy rộng loại 2 các bạn có thể tham khảo ví dụ dưới đây

Ảnh 6: Ví dụ minh họa tích phân suy rộng loại 2
Điều kiện hội tụ của tích phân suy rộng
Với mỗi loại tích phân suy rộng sẽ có những điều kiện riêng, cụ thể:
Điều kiện của tích phân suy rộng loại 1
Điều kiện hội tụ của tích phân suy rộng loại 1 cụ thể như sau:

Ảnh 7: Điều kiện hội tụ của tích phân suy rộng loại 1
Điều kiện của tích phân suy rộng loại 2
Điều kiện hội tụ của tích phân suy rộng loại 2 cụ thể như sau:
Về định nghĩa

Ảnh 8: Định nghĩa điều kiện hội tụ của tích phân suy rộng loại 2
Định lý về điều kiện hội tụ của tích phân suy rộng loại 2

Ảnh 9: Định lý về điều kiện hội tụ của tích phân suy rộng loại 2
Hệ quả của điều kiện hội tụ của tích phân suy rộng loại 2 được phát biểu như sau:

Ảnh 10: Hệ quả của điều kiện hội tụ của tích phân suy rộng loại 2
Trên đây là những kiến thức liên quan đến tích phân suy rộng, hy vọng sẽ giúp ích cho các bạn trong quá trình học tập. Chúc bạn ứng dụng giải toán thành công.
Nguồn ảnh: Internet



