Góc giữa đường thẳng và mặt phẳng là kiến thức nền tảng để bạn có thể học tốt môn toán hình ở trung học phổ thông, đặc biệt là ứng dụng vào giải các bài tập về hình học không gian. Bài viết này sẽ hệ thống lại toàn bộ kiến thức tổng quát về góc giữa đường thẳng và mặt phẳng cùng một số bài tập liên quan mà bạn có thể tham khảo.
-
Định nghĩa góc giữa đường thẳng và mặt phẳng
Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu vuông góc của nó lên trên mặt phẳng.
Nếu đường thẳng d vuông góc với mặt phẳng (P) thì ta nói góc giữa đường thẳng d và mặt phẳng (P) bằng 90 độ,
Nếu đường thẳng d không vuông góc với mặt phẳng (P) thì góc giữa đường thẳng d và mặt phẳng (P) là góc giữa đường thẳng d và hình chiếu d’ của nó lên mặt phẳng (P).
-
Cách xác định góc giữa đường thẳng và mặt phẳng
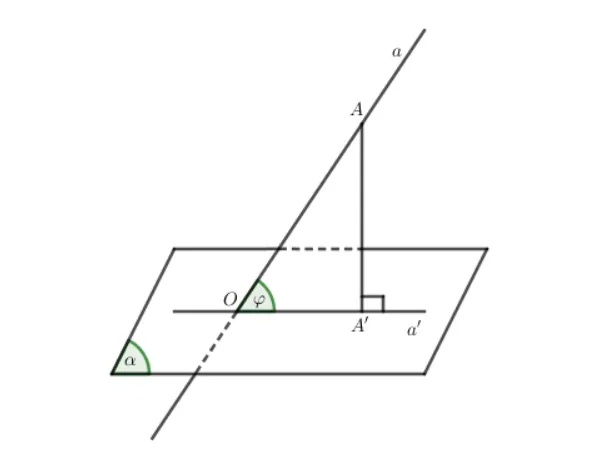
Hình minh họa (Nguồn: Internet)
Để xác định góc giữa đường thẳng a và mặt phẳng (![]() ) ta thực hiện các bước sau:
) ta thực hiện các bước sau:
- Bước 1: Tìm giao điểm O = a
- Bước 2: Dựng hình chiếu A’ của điểm A
- Bước 3: Góc chính là góc giữa đường thẳng a và mặt phẳng
Lưu ý: Để dựng hình chiếu A’ của điểm A lên mặt phẳng ta chọn một đường thẳng khi đó AA’//b
-
Phương pháp tính góc giữa đường thẳng và mặt phẳng
Để tính góc giữa ta sẽ sử dụng hệ thức lượng trong tam giác vuông OAA’. Ngoài ra, bạn có thể áp dụng công thức sau để tính góc ![]()
Trong đó:
là VTCP của đường thẳng a,
là vectơ có giá vuông góc với mặt phẳng
-
Một số bài toán tính góc giữa đường và mặt phẳng
Bài tập 1: Cho tam giác ABC vuông cân tại A có BC = a. Trên đường thẳng qua A vuông góc với mặt phẳng (ABC) lấy điểm S sao cho . Yêu cầu: Tính số đo góc giữa đường thẳng SA với mặt phẳng (ABC)
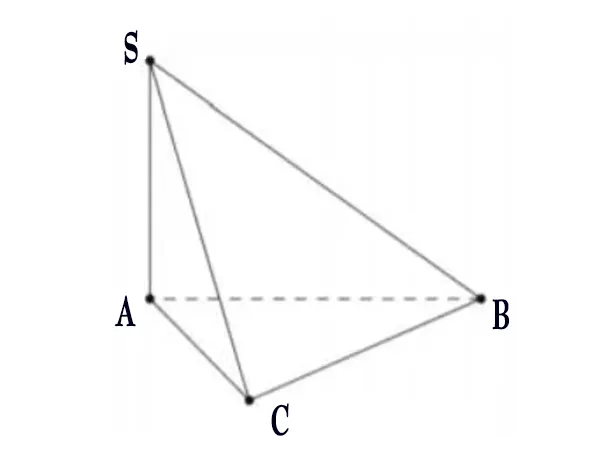
Hình minh họa (Nguồn: Internet)
Bài giải:
Ta có:
Bài tập 2: Cho và (P): 2x - y + 2z + 1 = 0.
Yêu cầu tìm m để
Bài giải:
có một VTCP
(P) có một VTCP
Bài tập 3: Cho hình chóp S.ABC có đáy là tam giác vuông ABC (cạnh huyền BC = a). Hình chiếu vuông góc của S lên mặt phẳng (ABC) trùng với trung điểm của đoạn BC. Cho biết SB = a. Yêu cầu tính số đo của góc giữa đoạn SA với mặt phẳng (ABC).
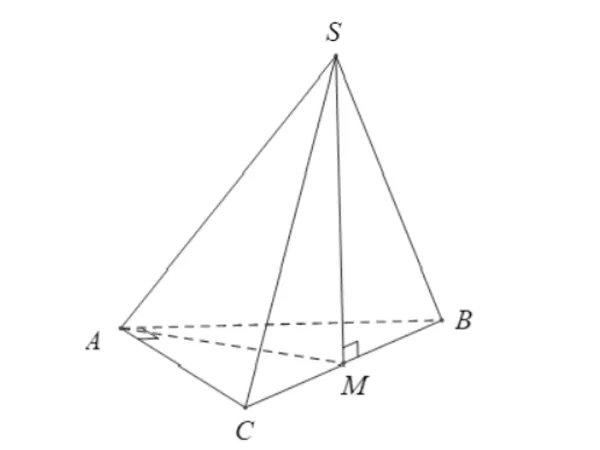
Hình minh họa (Nguồn: Internet)
Bài giải:
Gọi M là trung điểm cạnh BC
Tam giác ABC vuông tại A có đường trung tuyến AM
Suy ra: AM = BM = , SB = a (đề bài cho)
Ta có SM vuông góc với mặt phẳng (ABC) => AM là hình chiếu của SA lên mặt phẳng (ABC).
=>
Áp dụng định lý Pytago ta được:
Xét tam giác SAM ta có:
Bài tập 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh (AB = BC= CD = AD). Biết đường thẳng SA vuông góc với mặt phẳng đáy (SA= a). Góc giữa đường thẳng SC và mặt phẳng (SAB) là . Yêu cầu tan =?
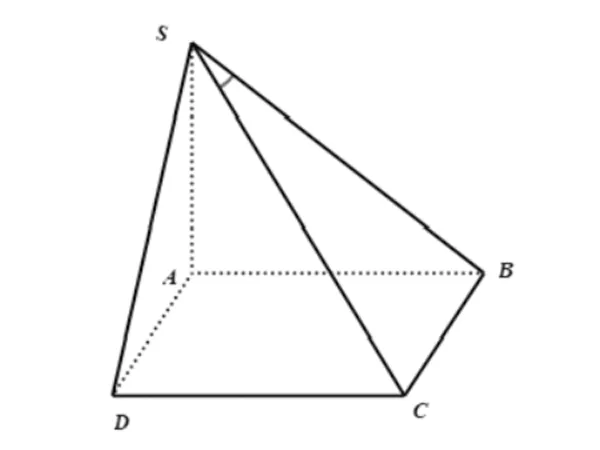
Hình minh họa (Nguồn: Internet)
Bài giải:
Ta có: S là hình chiếu của S lên (SAB) (1)
Mặt khác ta có: BC AB (tính chất của hình vuông) và BC SA (vì SA)
Suy ra: BC
=> B là hình chiếu của C lên mặt phẳng (SAB) (2)
Từ (1) và (2) suy ra
Xét tam giác SAB vuông tại A, ta có:
Xét tam giác SBC vuông tại B, ta có:
Bên trên là những kiến thức tổng quát và một số dạng bài toán thường gặp của góc giữa đường thẳng và mặt phẳng. Hy vọng qua bài viết bạn đã có thể nắm chắc khái niệm, cách tính và xác định góc giữa đường thẳng và mặt phẳng.



